The intermediate field lattice

If I have two fields and , and , we call a subfield of , but it turns out the proper way to think of it is the reverse. We don’t think of as some starting field with as a smaller one sitting inside. Instead, we think of as the starting field, and as a field extension of . We could do this for any object, but for whatever reason, it works well in Galois theory.

So one thing we could ask is “what are all the fields between and ? We can draw nice pictures called Hasse diagrams. The idea is, we put the bigger fields towards the top, and make it so that fields that contain each other are connected by a chain of lines.

Let’s do an example. Suppose we start with and extend it to the field . Here’s the picture:

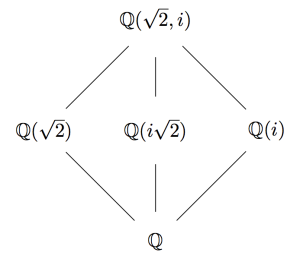You forgot about , didn’t you? Yeah, it’s hard. Man, if only there was a way to make sure we got all of them. Like, putting them in a one-to-one correspondence with, I don’t know, groups or something like that.

But seriously, how do we know we got everything? Well, degree 2 extensions can always be written as adjoining the square root of something (fun exercise I alluded to previously), and we can check that these are the only possibilities that lie inside . Since , all the extensions need to be of degree 1,2, or 4. Since 1 and 4 are stupid, we need only consider the degree 2 extensions, and we just checked that we got them all.

One more thing: the fact that is on the left and is on the right is arbitrary. I could order those three fields in any of the 6 different ways, and it would still be correct. My choice was arbitrary. All that matters is the containment relationships.